数学杂项——有时候可以关乎一个奖牌的东西
作者:老陈
例1——饥饿序列 (Codeforces 327B)
时间限制:1s 内存限制:256MB
题目描述
lahub和lahubina去一家豪华餐厅约会。一切都很好直到结账。服务员要的不是钱,而是让lahub写一个带有n个数的饥饿序列。
一个包含n个正整数的序列$a_1,a_2,…,a_n$是个饥饿序列当且仅当:
序列单调递增
对于序列中任意两个数,均不能整除。
lahub遇到了麻烦,所以他向你求助。帮帮他!
输入描述
仅包含一个正整数n。($1≤n≤10^5$)
输出描述
输出一行包含n个数代表一个可能的饥饿序列$a1,a2,…,an(1≤ ai ≤ 10^7 )$
如果有多个符合要求的序列,请输出任意一个
| Sample Input | Sample Output |
|---|---|
| 3 | 2 9 15 |
| 5 | 11 14 20 27 31 |
分析
对于题目描述,我们可以发现一个很关键的地方:
对于序列中任意两个数,均不能整除即一个数不可能成为另外一个数的因子。
但注意并不是一定互质。例如:9 12
但是,很明显,质数序列肯定符合这个要求。
所以仅需输出质数序列的前n项即可。
获得质数序列可以使用素数筛,不再赘述。
例2——士兵与数字游戏(Codeforces 546D)
时间限制:3s 内存限制:256MB
题目描述
两个士兵在玩游戏。一开始,他们中的一个选择了一个正整数 n 并把它给第二个士兵。然后第二个士兵会在每一回合尝试找到最大的数。每一轮包括选择一个正整数 x > 1,使 n 能被 x 整除,并将 n 替换为 n / x 。当 n 等于 1,并且没有更多可能有效的移动时,游戏结束,第二名士兵的得分等于他执行的回合数。
为了使游戏更有趣,第一名士兵选择的 n 是 a!/b!(这里的a和b是正整数且 $a ≥ b$)。
第二名士兵的最高分是多少?
输入描述
第一行包含一个正整数t ,代表第二个士兵玩的游戏场数。($1≤ t ≤10^6$)
接下来 t 行,每行输入两个正整数a 和 b($1 ≤ b ≤ a ≤5×10^6$),代表游戏中的整数n。
输出描述
对于每场游戏输出第二个士兵的最大得分。
Sample Input
2
3 1
6 3
Sample Output
2
5
分析
我们容易知道,这是一道求质因子个数的题目。
对于一个数 n ,我们的 x 一直取 n 的质因子就可以得到最高分。
但是,
$$
𝑛=\frac{a!}{𝑏!}=(𝑏+1)(𝑏+2)…(𝑎−1)𝑎
$$
那么,对于一个问题,答案就是从 b+1 到 a 的所有数的质因子个数之和。
那么,对于一个问题,答案就是从 b+1 到 a 的所有数的质因子个数之和。
那么,怎么求一个数的质因子个数呢?
首先,质数因子嘛,要求一下质数表。
然后对于这个数,从2开始一个一个试除,能整除就质因子个数+1。
考虑一下最差情况,
$$
t= 10^6, b=1, a= 5×10^6
$$
我们需要对 $ 5×10^6 $个数求质因子个数 ,假设求因子个数的时间复杂度是O(1)(并不是)
个数求质因子个数 ,假设求因子个数的时间复杂度是O(1)(并不是)
,我们需要进行 $5×10^{12}$次运算。明显超时。
有没有更好的做法?
我们可以模仿素数筛的做法来得到 [1, $5×10^6$]的所有数的因子数。
对于每个询问区间,我们可以用前缀和处理一下。
对于一次询问,我们只需O(1)即可解决。
对于最差情况,我们仅需大约$1.1×10^8$次运算即可,符合时间要求。
1 | |
例3——密码486
时间限制:5s 内存限制:128MB
题目描述
Bob每戒一次烟,就会更换电子邮件的密码。密码总以no-smokX的形式设置。X则是个位数以上的自然数。不仅如此,第k次戒烟时,Bob会选择具有k个约数的数值X。例如,第12次戒烟时修改的密码是no-smok486。486有1、2、3、6、9、…、243、486共12个约数。
有一天,Bob睡觉前下定决心要戒烟,并修改了邮箱密码。第二天清晨,他发现自己忘记了新设定的密码,只记得密码中的数值具有n个约数,且取值范围是[l,r](包含l和r)。
试编写程序,计算取值范围内共有几个可能的密码。
输入描述
第一行包含一个正整数t ,代表测试用例个数。($1≤ t ≤ {50}$)
接下来 t 行,每行输入三个正整数n、l 和 r($n < 400,1 ≤ l ≤ r ≤1×10^7,r-l < 1×10^6 $)。
输出描述
对于每个测试用例,输出答案。
Sample Input
3
2 2 10
12 486 486
200 1000000 2000000
Sample Output
4
1
19
本题要求的是[l,r]中有多少个数的约数个数是n。
本题的重点在于如何快速求约数个数。
约数个数公式:
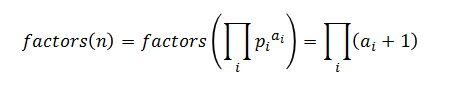
我们发现这里用到了质因数分解。所以我们可以使用上一题的质因数分解来做。
总时间复杂度O(t(r-l)+nloglogn),最差情况下运算次数大约为$1×10^8$次,符合要求。
更简便的做法:
1 | |
乍一看,貌似会超时?
这段代码的时间复杂度是O(n logn)
即总时间复杂度O(t(r-l)+nlogn),最差情况下运算次数大约为$3.2×10^8$次,符合要求。
例4——2^x mod n = 1(HDU 1395)
时间限制:1s 内存限制:64MB
题目描述
给定一个整数N,求最小的 x (x > 0)使得$2^x mod n=1$。
输入描述
输入包含多组测试用例,每个测试用例包含一个正整数N。
输出描述
若存在最小的 x,请输出“2^xmod n = 1”;否则输出“2^?mod n = 1”。
| Sample Input | Sample Output |
|---|---|
| 2 | 2^? mod n = 1 |
| 5 | 2^4 mod 5 = 1 |
此题暴力可A,不再赘述。(可能是数据水)
但是数据一大,暴力就不行了。
欧拉函数:$φ(n)——[1,n]$内与n互质的数的个数。
当n为质数时,$φ(n)=n-1$。
当$n=p^k$时(p是素数),$φ(n)=φ(p^k )=p^k-p^{k-1}=(p-1)p^{k-1}$
若n,m互质,$φ(nm)=φ(n)φ(m)=(n-1)(m-1)$
若n是奇数,则$φ(2n)=φ(n)$
由上面的性质,我们可以写出求欧拉函数的一般式:
我们设正整数n的唯一分解为$p_1^{a_1} p_2^{a_2 }…p_i^{a_i }$。其中,$ p_1,p_2,…,p_i$为素数。
则我们可以得到:
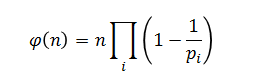
两个重要定理:
- 当a与n互质时:
$$
𝑎^{𝜑(𝑛)} 𝑚𝑜𝑑 𝑛=1(欧拉定理)
$$
- 当a与n互质且n为质数时:
$$
𝑎^{𝑛−1} 𝑚𝑜𝑑 𝑛=1(费马小定理)
$$
延伸:
小于n且与n互质的数的和:
$$
\frac{φ(n)∗n}2 (n>1)
$$
应用:
求$7^{222}$的个位数。
因为7和10互质,且$φ(10)=4$
所以$7^4 mod 10=1$
所以$7^{222} mod 10=7^{4∗55}∗7^2 mod 10=7^2 mod 10=9$
即$7^{222} mod 10=7^{222\%4} mod 10=7^2 mod 10=9$
因为涉及唯一分解,那就与前面一样进行分解,边分解边计算即可。
1 | |
解题——2^x mod n = 1
回到正题。
首先,我们能确定n=1时肯定无解。
对于n为偶数,我们知道$2^x$肯定是个偶数,那么模一个偶数的结果不可能是1。
所以当n为偶数时同样无解。
对于n为奇数,我们根据欧拉定理可以知道$φ(n)$是符合题目要求的一个数。所以n为奇数时一定有解。
但是,题目要求x最小,但是$φ(n)$不一定是最小值。
我们假设r是问题的解,即r是最小的x使得$2^x \mod n=1$。
那么对于其他的数X,若有$2^X \mod n=1$。
那我们可以得到$X \mod r=0$。
所以,我们可以遍历$φ(n)$的所有因子就可以得到答案。
模运算
模运算的运算律:
加法:
$(a+b)\mod n=(a \mod n+b \mod n)\mod n$
减法:
$(a-b)\mod n=(a \mod n-b \mod n)\mod n$
乘法:
$(a∗b)\mod n=(a \mod n∗b \mod n)\mod n$
幂:
$a^b \mod n=(a \mod n)^b mod n$
注意!除法不成立。
那么,如何计算$(a/b)\mod n$?
我们可以通过将除b转换成乘b的逆元来解决,即$(a∗b^{-1} )\mod n$ 。
逆元
逆元的定义:
$bc \mod p≡1$
此时c称为b的逆元。
容易知道,只有b和p互质的时候,c才有解;否则无解。
那么c怎么求?
联想费马小定理:
$a^{n-1} ≡1(mod n)$
我们可以得到:
$b∗b^{n-2} ≡1(mod n)$
即$c=b^{n-2} $ 。
推荐练习
| Codeforces | 洛谷 |
|---|---|
| 755A | P1036 |
| 948B | P1075 |
| 1047C | P1125 |
| 432C | P1832 |
| 236B | P2398 |
| 385C | P3383 |
| 151C | P2424 |
| 327C | P1306 |
| 615D | P1405 |
| P3811 |
