LCS&&LIS

|

最长公共子序列&&最长递增子序列

作者：肖锐

LCS—最长公共子序列


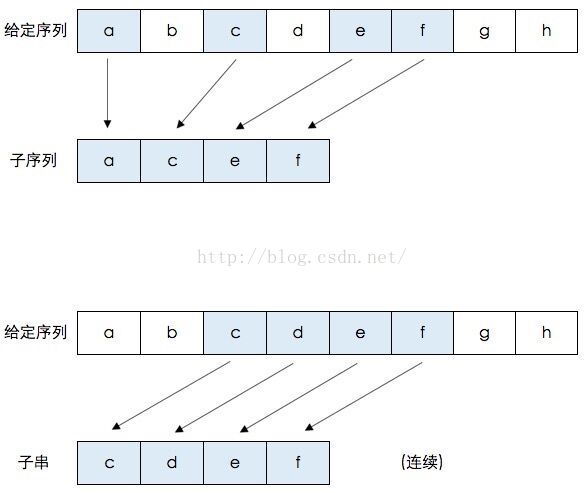
最长公共子序列不需要连续

给定序列
s1={3,5,7,4,8,6,7,8,2}
s2={1,3,4,5,6,7,7,8}
s1和s2的相同子序列，且该子序列的长度最长，即是LCS
s1和s2的其中一个最长公共子序列是 {3,4,6,7,8}

动态规划法求LCS

动态规划算法通常用于求解具有某种==最优性质==的问题。
在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有==最优值==的解
例如LCS中的‘最长’

动态规划法的基本思路

  1. 动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
  2. 若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。
  3. 如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算
  4. 将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策。换句话说，每个状态都是过去历史的一个完整总结，这就是无后效性

    三个特点：最优子结构、重叠子问题、无后效性

递归求斐波那契数列

数列：1、1、2、3、5、8、13、21、34、……

1
2
3
4
5
6
7
8
9
int f(int n)
{
    if(n == 0) return 0;
    if(n == 1 ) return 1;
    if(n >= 2)
    {
        return f(n-1)+f(n-2);
    }
}

这种算法并不高效,它做了很多重复计算,它的时间复杂度为$O(2^n)​$


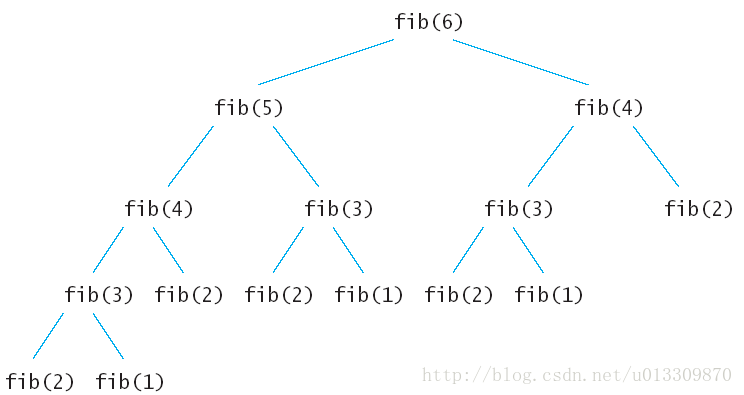
在斐波拉契数列，可以看到大量的重叠子问题，比如说在求fib(6)的时候，fib(2)被调用了5次。如果使用递归算法的时候会反复的求解相同的子问题，不停的调用函数，而不是生成新的子问题。

动规求斐波那契数列

使用动态规划来将重复计算的结果具有”记忆性”,就可以将时间复杂度降低为O(n)

1
2
3
4
5
6
7
8
void f()
{
    int f[10];
    f[0] = 0;
    f[1] = 1;
    for(int i = 2; i <= 10; i++)
        f[i] = f[i-1] + f[i-2];
}

100

回到原题，求解LCS

解决LCS问题，需要把原问题分解成若干个子问题，所以需要刻画LCS的特征
设S1={A0,A1, … ,Am}，S2={B0,B1, … Bn}，它们LCS为Z={Z1,Z2, … ,Zk}

  1. 如果Am=Bn，则Zk=Am=Bn，且{Z1, Z2, …, z(K-1)}是{A0,A1, … ,A(m-1)}和{B0,B1, … B(n-1)}的一个最长公共子序列


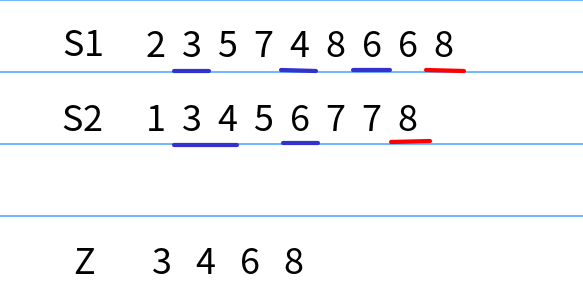
即假如S1的最后一个元素 与S2的最后一个元素相等，那么S1和S2的LCS就等于 {S1减去最后一个元素} 与 {S2减去最后一个元素} 的 LCS 再加上 S1和S2相等的最后一个元素

设S1={A0,A1, … ,Am}，S2={B0,B1, … Bn}，它们LCS为Z={Z1,Z2, … ,Zk}

  1. 如果Am!=Bn

    • 若Zk!=Am，则{Z1,Z2, … ,Zk}是{A0,A1, … ,A(m-1)}和{B0,B1, … Bn}的一个最长公共子序列

    • 若Zk!=Bn，则{Z1,Z2, … ,Zk}是{A0,A1, … ,Am}和{B0,B1, … B(n-1)}的一个最长公共子序列

假如S1的最后一个元素 与 S2的最后一个元素不等，那么S1和S2的LCS就等于 ： MAX( {S1减去最后一个元素} 与 S2 的LCS， {S2减去最后一个元素} 与 S1 的LCS)

动态转移方程

假设我们用C[i,j]表示Xi 和 Yj 的LCS的长度（直接保存最长公共子序列的中间结果不现实，需要先借助LCS的长度）。其中X = {x1 … xm}，Y ={y1…yn}，Xi = {x1 … xi}，Yj={y1… yj}。
可得动态转移方程如下：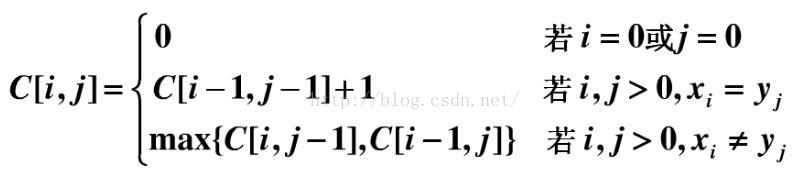

s1={1,3,4,5,6,7,7,8}，s2={3,5,7,4,8,6,7,8,2}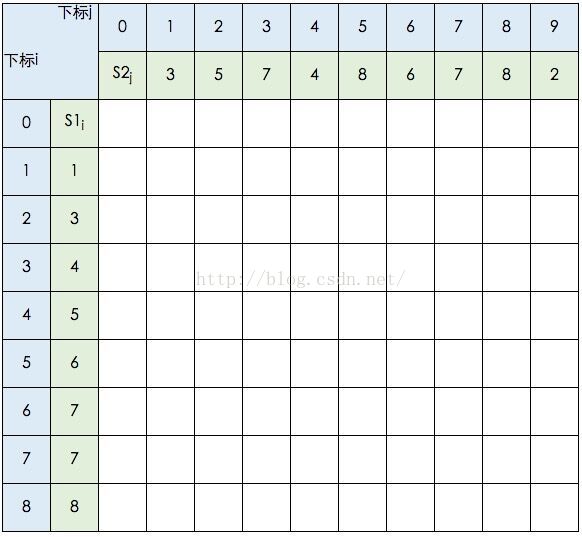

图中的空白格子需要填上相应的数字（这个数字就是C[i,j]的定义，记录的LCS的长度值）。填的规则依据公式，简单来说：如果横竖（i,j）对应的两个元素相等，该格子的值 = c[i-1,j-1] + 1。如果不等，取c[i-1,j] 和 c[i,j-1]的最大值。

首先初始化该表。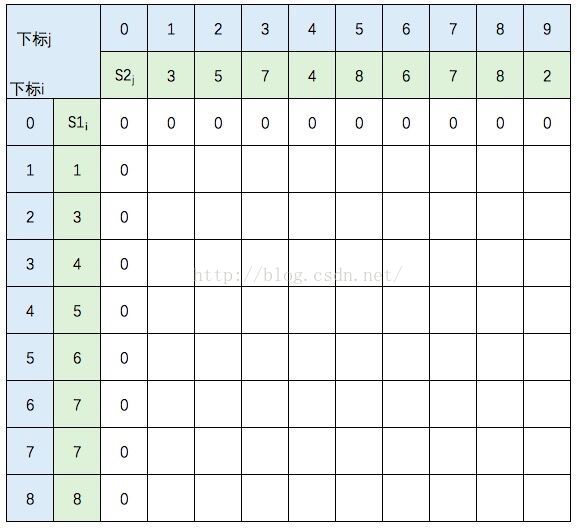

当i=2，j=1时，S1的元素3 与 S2的元素3 相等，所以 C[2,1] = C[1,0] + 1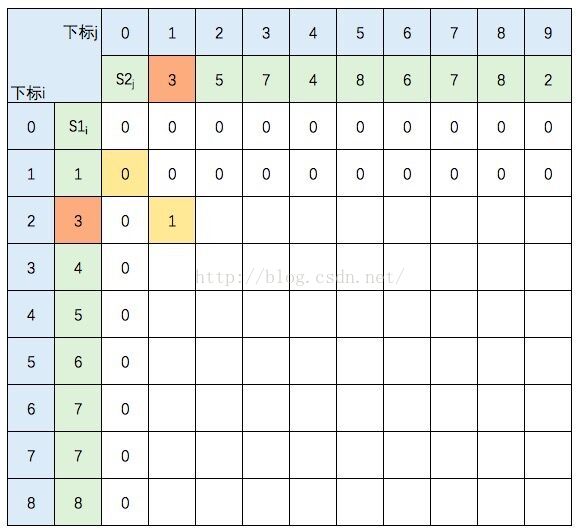

当i=2，j=2时，S1的元素3 与 S2的元素5 不等，C[2,2] =max(C[1,2],C[2,1])
图中C[1,2] 和 C[2,1] 背景色为浅黄色。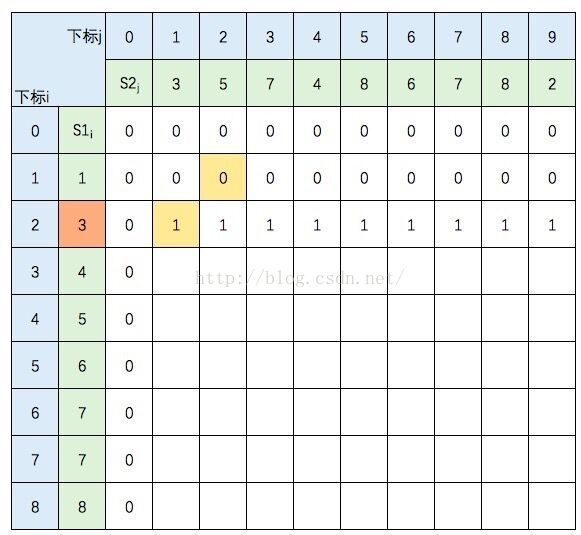


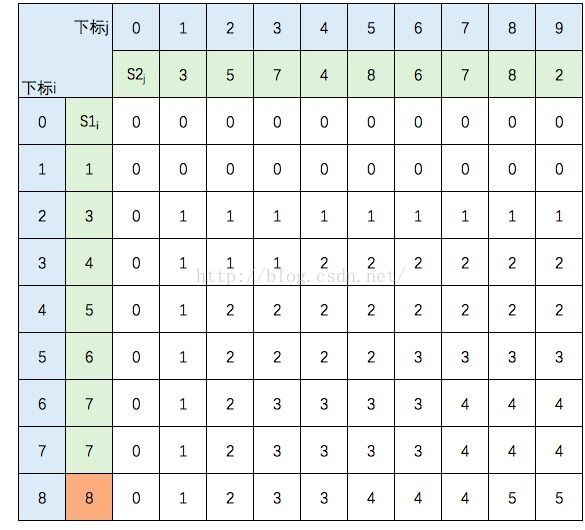
根据性质，c[8,9] = S1 和 S2 的 LCS的长度，即为5

模板题–POJ1458(Common Subsequence)

80%
题意：输入不定行，每行两个字符串，求每一行两个字符串的最长公共子序列长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const int MAXDP = 1e3;
const int MAXS = 1e7;
int dp[MAXDP][MAXDP];
char s1[MAXS], s2[MAXS];
int LCS(char* s1, char* s2)
{
    int len1 = strlen(s1) - 1;//因为s1,s2是从1开始存的，所以长度要减1
    int len2 = strlen(s2) - 1;
    for(int i = 0; i <= len1; i++)
        for(int j = 0; j <= len2; j++)
        {
            if(i == 0 || j == 0)	
            	dp[i][j] = 0;
            else if(s1[i] == s2[j])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
        return dp[len1][len2];
}
int main()
{
    s1[0] = ' ', s2[0] = ' ';
    while(cin >> s1 +1 >> s2 + 1)
        cout << LCS(s1, s2) << endl;
    return 0;
} //时间复杂度：O（len1*len2)

LCS进阶

  1. 还原最长公共子序列、记录路径：HDU1503(Advanced Fruits)
  2. LCS变形：
  3. poj 1159 Palindrome LCS一维滚动数组优化

最长公共子串（连续）

和LCS区别是区别就是因为是连续的，如果两个元素不等，那么就要=0了而不能用之前一个状态的最大元素

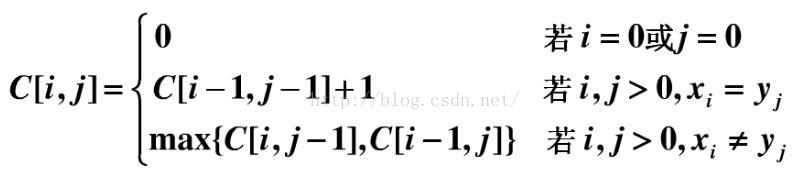
LIS–最长递增子序列

假设有序列A = {5, 2, 8, 6, 3, 6, 9, 7}
其递增子序列有：{5,8,9}, {2,6,9}, {5,6,7}……
其中，最长递增子序列为{2, 3, 6, 9}和{2, 3, 6, 7}

动态规划求LIS

设dp[i]表示以i结尾的子序列中LIS的长度，dp[j] (0<= j < i) 来表示在i之前的LIS的长度
有一序列A={5, 3, 4, 8, 6, 7}

进一步分析

d(i) = max{ 1, d(j)+1} ,且满足A[i] >= A[j]

  1. max显然是为了找到最长的满足条件的序列，容易理解
  2. 在max里面加入1作为比较的一员，是因为，最坏的情况就是序列是单调递减的，那么每个数都可以算是一个子序列，一个数的长度当然为1
  3. d[j]为什么要加1呢，因为比较的数A[i] > A[j]，那么A[i]就是最长子序列的一员，所以直接在d[j]上加1

模板题–HDU1257-最少拦截系统

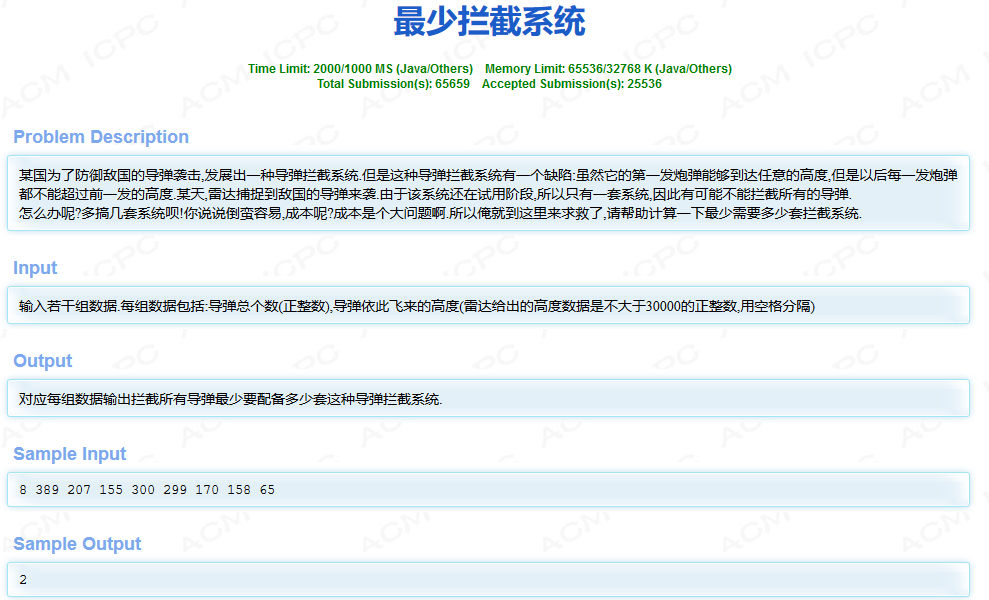
解题

我们所求的拦截系统的数目其实就是一个序列的所有递减子序列，并使其数量尽量减少，然后递减子序列的数目又会等于最长上升子序列中所含元素的个数；不理解的话可以去看下下面的test

1
2
3
4
5
6
7
8
9
Input
8 389 207 155 300 299 170 158 65
1 100
6 300 200 400 200 100 500
8 500 300 400 200 300 100 200 50
8 500 300 400 200 80 200 100 50
8 500 300 400 200 80 500 100 50
Output
213223
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int dp[100000], arr[100000], len;
int LIS()
{
    memset(dp, 0, sizeof(dp));
	int MAX = -1e9;
	for(int i = 1; i <= len; i++)
		for(int j = 0; j < i; j++)
        {
			if(arr[i] > arr[j] && dp[i] < dp[j] + 1)
			{
				dp[i] = dp[j] + 1;
				if(dp[i] > MAX)
					MAX = dp[i];
			}
        }
	return MAX;
}

int main(){
	while(cin >> len)
    {
		for(int i = 1; i <= len; i++)
			cin >> arr[i];
		cout << LIS() << endl;
	}
    return 0;
}//时间复杂度:O(n^2)

LIS进阶

  1. 算法优化：NlogN时间复杂度–可参考(20:41开始)

    HRBU ACM 01背包 LIS 拓扑 凸包—-bilibili

  2. 最大递增子数组和–由LIS O(n2)的办法变化而来的，对应的模板题：

    HDU1087(Super Jumping! Jumping! Jumping!)

  3. LIS变形：